Aula 22: Algoritmos

Algoritmo

Um algoritmo é uma descrição de um método de resolver um problema. A palavra vem do nome de um matemático, Mohammed ibn-Musa Al-Khowarizmi, que viveu no Baghdad nos anos 780 - 850 dC.

Ordenar

Para as nossas aulas isto significa que vamos conceber um método de atacar um problema mesmo sem mexer com o computador. Como exemplo vamos desenhar uma solução para ordenar um array de números. Imagine que temos um array de N integers. Como vamos atacar este problema?

A figura mostra um array de 10 elements a ordenar.

Sem olhar nos detalhes (para já), podemos haver as seguintas soluções:

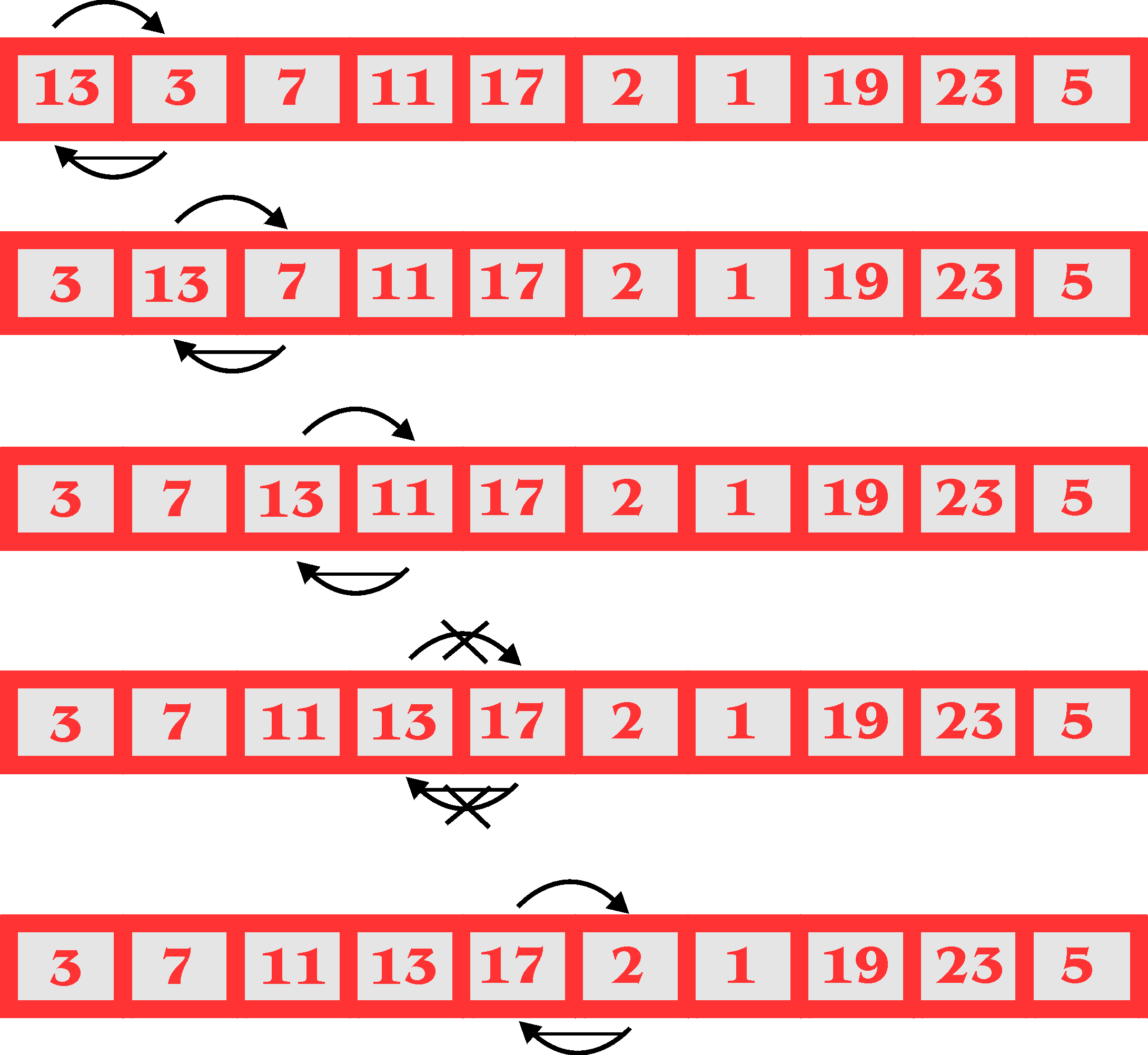
Olhar na lista. Se dois números consecutivos não estão ordenados corectos vamos trocar-os. Repete isto até a lista está ordenada. A figura abaixa mostra um exemplo com os primeiros passos.

Procura na lista o elemento mais pequeno. Põe este número no primeiro lugar. Depois procura o mínimo no resto dos números. Põe este número no segundo lugar. Repete isto N vezes e o array estará ordenado. A figura abaixa mostra os primeiros passos para o nosso array.

Bubble sort

Isto são dois algoritmos para ordenar um array. O primeiro chama-se "Bubble sort" (bubble = bolha, sort = ordenar), porque parece bolhas de ar na água que vão lentemente para o superfície. Vamos implementar esta idea em PASCAL. Ao primeiro ]e útil desenhar um flow diagram (diagrama de fluxo).

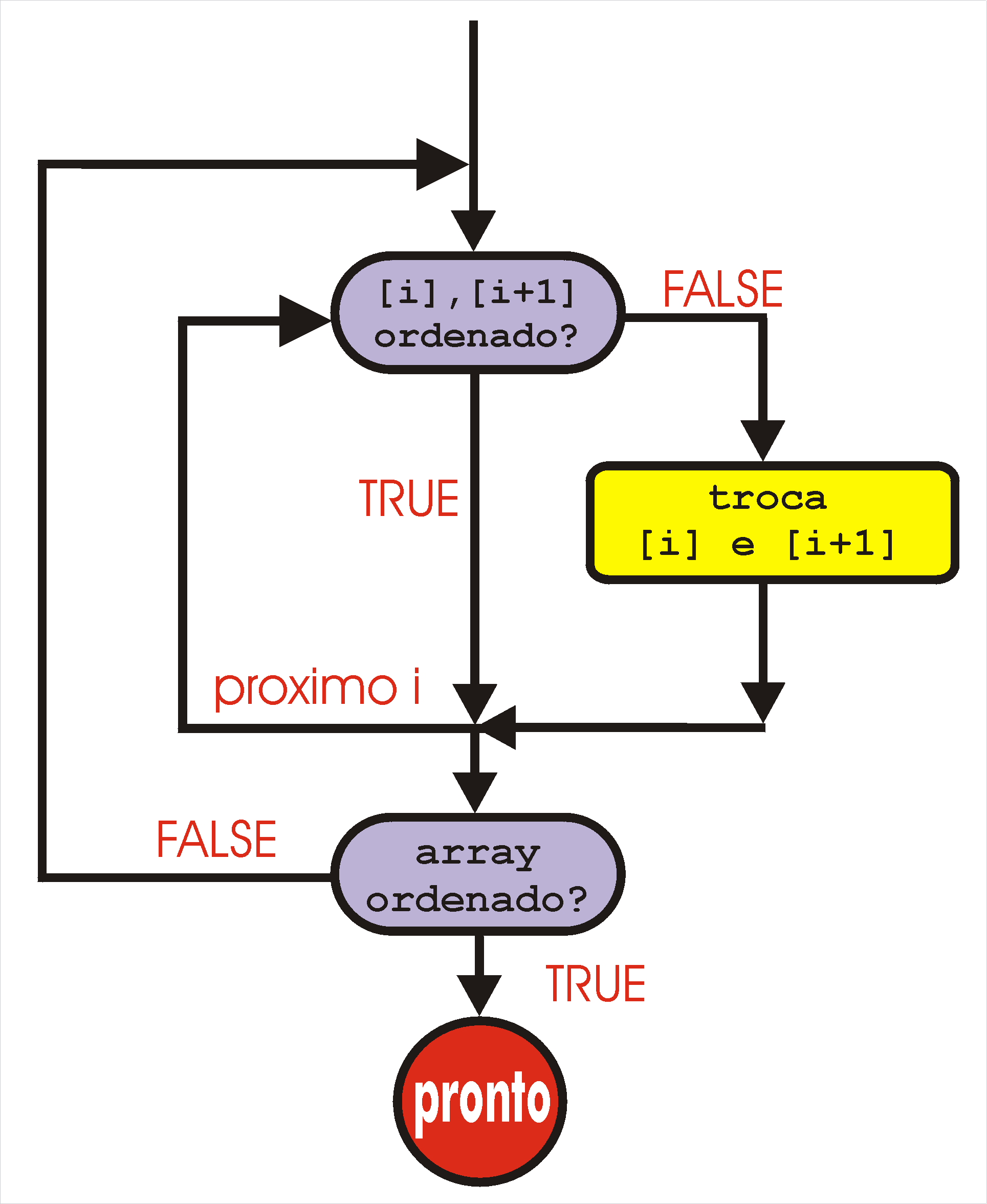Diagrama de fluxo do algoritmo Bubble sort.
[i] significa elemento i do array.

Neste diagrama de fluxo já consegimos reconhecer a primeira idea de um programa PASCAL. Já é possível distinguir dois ciclos, um ciclo que verifica uma vez a ordenação de todos os pares de números e o outro ciclo que repete estes passos do array até TUDO está correcto. Além disso temos uma instrução para trocar dois números e uma instrução que verifica que dois números seguidos estão ordenados.
Agorá estamos na altura de implementar os promenores. Vamos programar os três partes distintas da figura acima. Assume que existe um array com nome n[1..N].

1) Para verificar se dois números seguidos estão ordenados correcto:
if n[i] < n[i+1] then ...

2) Trocar dois números também não é difícil. Por exemplo assim:
n[i] := n[i] + n[i+1];
n[i+1] := n[i] - n[i+1];
n[i] := n[i] - n[i+1];
Embora de funcionar (verifica isto!), este método é um pouco desajeitado. Normalmente trocar dois números fazemos com a ajuda de uma variável suplementar que vai guardar informação temporariamente:
temp := n[i];
n[i] := n[i+1];
n[i+1] := temp;

3) Para verificar que o array está ordenado completamente precisa-se uma variável que vai guardar a informação se houve uma mudança no último passo do array. Vamos declarar uma variável change que será TRUE se houve uma troca de dois números.

Com isto o procedimento inteiro é:

repeat
change := FALSE; (* até já ainda não houve trocas *)
for i := 1 to N-1 do (* verifica todos os apres seguidos: *)
    if n[i]>n[i+1] (* não ordenado? *)
      begin
          (* troca os dois números: *)
        temp := n[i];
        n[i] := n[i+1];
        n[i+1] := temp;
          (* faça um signal: *)
        change := TRUE;
      end;
until NOT change;

Velocidade / Eficiência

Na análise do nosso algoritmo é também possível dizer alguma coisa da eficiência do mesmo. Qual será o tempo de execução, no mínimo, no máximo, na média. Se assumimos que o tempo de execução é proporcional com o número de vezes o programa tem de ler um elemento do array podemos concludir o seguinte:

O algoritmo Bubble sort deve

no mínimo fazer um passo do array, então ler 2*(N-1) números
no máximo fazer N-1 passos do array, então ler 2*(N-1)² números.
a média: N²-N (a média dos números acima)

com N o tamnho do array.
Em comparação, o outro algoritmo (Scan sort) deve

no mínimo fazer N passos do array, mas cada vez pode ler menos elementos (a primeira vez tem de ler todos os N elementos, no segundo passo pode começar com elemento 2, depois com elemento 3, etc.), por isso deve ler N + (N-1) + (N-2) + (N-3) ... 1 = N²/2 números
o programa sempre deve ler o mesmo número de elementos, indepedente da distribução dos números. Por isso, no máximo também deve ler N²/2 vezes.
e a média fica assim N²/2.

Qual algoritmo é mais eficiente? Para arrays com um grande número de elementos, por exemplo N=100, o segundo algoritmo seria cada vez mais eficiente (5000 vs. 9900). Também nota que no algoritmo Bubble sort temos de trocar mais números. Porquê? É fácil mostrar isto. Se um número está completamente no outro lado da lista temos de deslocar este número para o outro lado do array, isto torna o programa muito lento, com N-1 trocas. Com o outro algoritmo, o elemento seria trocada só uma vez. De facto, Bubble sort é provavelmente um dos piores algoritmos. O mais eficiente provavelmente é Quick-sort (fora do âmbito desta cadeira). A razão para mostrar o Bubble sort aqui é que este algoritmo é muito elegante e serve para mostrar ordenações e algoritmos em geral.

Peter Stallinga. Universidade do Algarve, 6 Maio 2002